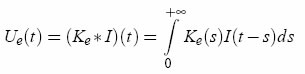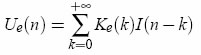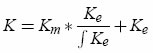| Presentation |
| People |
| Publications |
| Internal space |
A postdoc position is available in the UNIC group.
The HR-CORTEX project is funded by the French ANR.
|
Active Electrode Compensation (AEC) AEC is a digital technique of electrode compensation for intracellular recordings with a single electrode. It is presented in details in the following article (and supplementary material):
The electrode is represented by an unknown complex linear circuit, characterized by a kernel which we determine by injecting a noisy current. The method consists of two parts: 1) finding the electrode kernel, and 2) using the kernel to compensate the recordings. Compensation When recording intracellularly with a single electrode and injecting current at the same time, the recorded potential is Vr = Vm + Ue, where Vm the membrane potential and Ue is the voltage across the electrode. AEC relies on the idea that the electrode can be represented by a general linear filter with impulse response Ke(t). When this filter is known (see below), the voltage across is the electrode Ue(t) is calculated by computing a convolution with the input current I(t):
and the membrane potential Vm(t) is simply recovered from the recording Vr(t) by a subtraction: Vm(t)=Vr(t)-Ue(t). In practice, all signals are digitally sampled and the convolution is a sum:
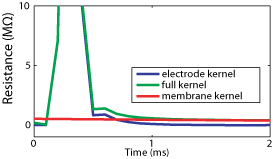
and the membrane potential is Vm(n)=Vr(n)-Ue(n). Only the first M terms of the sum are calculated (typically about 50), because the electrode kernel Ke vanishes after a couple of ms. In current-clamp, compensation with AEC can be done offline if both Vm(t) and I(t) are recorded. In dynamic-clamp or voltage-clamp, compensation has to be done online in real time because of the feedback. Estimation of the electrode kernel The electrode kernel must be estimated prior to any stimulation, as in standard bridge compensation (except this is an automatic procedure). The procedure runs in current-clamp mode, thus it can be done offline. Estimation of the full kernel K The electrode must be estimated intracellularly, because its properties can change after impalement. We start by estimating the kernel K for the full system (electrode + neuron), then an algorithm is applied to extract the electrode kernel. The procedure is the following: 1. Record the response of the system Vr(n) to a white noise current I(n) (typical duration: 10s ; the current is a series of independent random steps with zero mean and uniform distribution, typically -0.5 to 0.5 nA). 2. Determine the vector (K(0),...,K(m-1),V0) (V0 = resting potential) which gives the best linear approximation:
A fast linear algebra algorithm is detailed in the article (ref. above ; see also the sample code). Extraction of the electrode kernel Ke
1. Estimate Km as an exponential function from the tail of the full kernel K. 2. Find Ke by deconvolution (algorithm based on the Z-transform detailed in the article ; see also the sample code). The estimation is refined by using several passes of the algorithm.
|