In a previous post, I argued that the way the brain works is not algorithmic, and therefore it is not a computer in the common sense of the term. This contradicts a popular view in computational neuroscience that the brain is a kind of a computer that implements algorithms. That view comes from formal neural network theory, and the argumentation goes as follows. Formal neural networks can implement any computable function, which is a function that can be implemented by an algorithm. Thus the brain can implement algorithms for computable functions, and therefore is by definition a computer. There are multiple errors in this reasoning. The most salient error is a semantic drift on the concept of algorithm, the second major error is a confusion on what a computer is.

Algorithms

A computable function is a function that can be implemented by an algorithm. But the converse “if a function is computable, then whatever implements this function runs an algorithm” is not true. To see this, we need to be a bit more specific about what is meant by “algorithm” and “computable function”.

Loosely speaking, an algorithm is simply a set of explicit instructions to solve a problem. A cooking recipe is an algorithm in this sense. For example, to cook pasta: put water in a pan; heat up; when water boils, put pasta; wait for 10 minutes. The execution of this algorithm occurs in continuous time in a real environment. But what is algorithmic about this description is the discrete sequential flow of instructions. Water boiling itself is not algorithmic, the high-level instructions are: “when condition A is true (water boils), then do B (put pasta)”. Thus, when we speak of algorithms, we must define what is considered as elementary instructions, that is, what is beneath the algorithmic level (water boils, put pasta).

The textbook definition of algorithm in computer science is: "a sequence of computational steps that transform the input into the output." (Cormen et al., Introduction to algorithms; possibly the most used textbook on the subject). Computability is a way to formalize the notion of algorithm for functions of integers (in particular logical functions). To formalize it, one needs to specify what is considered an elementary instruction. Thus, computability does not formalize the loose notion of algorithm above, i.e, any recipe to calculate something, for otherwise any function would be computable and the concept would be empty (to calculate f(x), apply f to x). A computable function is a function that can be calculated by a Turing machine, or equivalently, which can be generated by a small set of elementary functions on integers (with composition and recursion). Thus, an algorithm in the sense of computability theory is a discrete-time sequence of arithmetic and logical operations (and recursion). Note that this readily extend to any countable alphabet instead of integers, and of course you can replace arithmetic and logical operations with higher-order instructions, as long as they are themselves computable (ie a high-level programming language). But it is not any kind of specification of how to solve a problem. For example, there are various algorithms to calculate pi. But we could also calculate pi by drawing a circle, measuring both the diameter and the perimeter, then dividing perimeter by diameter. This is not an algorithm in the sense of computability theory. It could be called an algorithm in the broader sense, but again note that what is algorithmic about it is the discrete structure of the instructions.

Thus, a device could calculate a computable function using an algorithm in the strict sense of computability, or in the broader sense (cooking recipe), or in a non-algorithmic way (i.e., without any discrete structure of instructions). In any case, what the brain or any device manages to do bears no relation with how it does it.

As pointed out above, what is algorithmic about a description of how something works is the discrete structure (first do A; if B is true, then do C, etc). If we removed this condition, then we would be left with the more general concept of model, not algorithm: a description of how something works. Thus, if we want to say anything specific by claiming that the brain implements algorithms, then we must insist on the discrete-time structure (steps). Otherwise, we are just saying that the brain has a model.

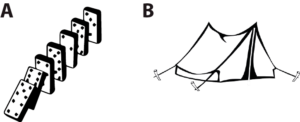
Now that we have more precisely defined what an algorithm is, let us examine whether the brain might implement algorithms. Clearly, it does not literally implement algorithms in the narrow sense of computability theory, i.e., with elementary operations on integers and recursion. But could it be that it implements algorithms in the broader sense? To get some perspective, consider the following two physical systems:

(A) are dominoes, (B) is a tent (illustration taken from my essay “Is coding a relevant metaphor for the brain?”). Both are physical systems that interact with an environment, in particular which can be perturbed by mechanical stimuli. The response of dominoes to mechanical stimuli might be likened to an algorithm, but that of the tent cannot. The fact that we can describe unambiguously (with physics) how the tent reacts to mechanical stimuli does not make the dynamics of the tent algorithmic, and the same is true of the brain. Formal neural networks (e.g. perceptrons or deep learning networks) are algorithmic, but the brain is a priori more like the tent: a set of coupled neurons that interact in continuous time, together and with the environment, with no evident discrete structure similar to an algorithm. As argued above, a specification of how these real neural networks work and solve problems is not an algorithm: it’s a model – unless we manage to map the brain’s dynamics to the discrete flow of an algorithm.

Computers

Thus, if a computer is something that solves problems by running algorithms, then the brain is not a computer. We may however consider a broader definition: the computer is something that computes, i.e., which is able to calculate computable functions. As pointed out above, this does not require the computer to run algorithms. For example, consider a box with some gas, a heater (input = temperature T) and a pressure sensor (output = P). The device computes the function P = nRT/V by virtue of physical laws, and not by an algorithm.

This box, however, is not a computer. Otherwise, any physical system would be called a computer. To be called a computer, the device should be able to implement any computable function. But what does it mean exactly? To run an arbitrary computable function, some parameters of the device need to be appropriately adjusted. Who adjusts these parameters and how? If we do not specify how this adjustment is being made, then the claim that the brain is a computer is essentially empty. It just says that for each function, there is a way to arrange the structure of the brain so that this function is achieved. It is essentially equivalent to the claim that atoms can calculate any computable function, depending on how we arrange them.

To call such a device a computer, we must additionally include a mechanism to adjust the parameters so that it does actually perform a particular computable function. This leads us to the conventional definition of a computer: something that can be instructed via computer programming. The notion of program is central to the definition of computers, whatever form this program takes. A crucial implication is that a computer is a device that is dependent on an external operator for its function. The external operator brings the software to the computer; without the ability to receive software, the device is not a computer.

In this sense, the brain cannot be a computer. We may then consider the following metaphorical extension: the brain is a self-programmed computer. But the circularity in this assertion is problematic. If the program is a result of the program itself, then the “computer” cannot actually implement any computable function, but only those that result from its autonomous functioning. A cat, a mouse, an ant and a human do not actually do the same things, and cannot even in principle do the same tasks.

Finally, is computability theory the right framework to describe the activity of the brain in the first place? It is certainly not the right framework to describe the interaction of a tent with its environment, so why would it be appropriate for the brain, an embodied dynamical system in circular relation with the environment? Computability theory is a theory about functions. But a dynamical system is not a function. You can of course define functions on dynamical systems, even though they do not fully characterize the system. For example, you can define the function that maps the current state to the state at some future time. In the case of the brain, we might want to define a function that maps an external perturbation of the system (i.e. a stimulus) to the state of the system at some future time. However, this is not well defined, because it depends on the state of the system at the time of the perturbation. This problem does not occur with formal neural networks precisely because these are not dynamical systems but mappings. The brain is spontaneously active, whether there is a “stimulus” or not. The very notion of the organism as something that responds to stimuli is the most naïve version of behaviorism. The organism has an endogenous activity and a circular relation to its environment. Consider for example central pattern generators: these are rhythmic patterns produced in the absence of any input. Not all dynamical systems can be framed into computability theory, and in fact most of them, including the brain, cannot because they are not mappings.

Conclusion

As I have argued in my essay on neural coding, there are two core problems with the computer metaphor of the brain (it should be clear by now that this is a metaphor and not a property). One is that it tries to match two causal structures that are totally incongruent, just like dominoes and a tent. The other is that the computer metaphor, just as the coding metaphor, implicitly assumes an external operator – who programs it / interprets the code. Thus, what these two metaphors fundamentally miss is the epistemic autonomy of the organism.