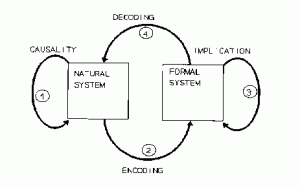
Robert Rosen was an influential theoretical biologist, who worked in particular on the nature of life. He made the point that living organisms are very special kinds of natural systems, in that they are anticipatory systems, which is the name of one of his most important books. He spends a substantial part of that book on epistemological issues, in particular on what a model is. The following figure is in my opinion a brilliant illustration of what a model is:

The natural system is what is being modeled. For example, the brain or the solar system. The formal system is the model, for example sets of differential equations describing Newtonian mechanics. The model has state variables that represent observables of the natural system. The mapping from the natural system to those state variables is called “encoding” here – it corresponds to measurement.  Decoding is the converse process. Causality describes changes occurring in the natural system, while implication describes changes in the formal system. A good model is one that is such that this diagram commutes. That is, causality in the natural system corresponds to implication in the formal system.

Let us apply this framework to the debate at hand: rate-based vs. spike-based theories of the brain. The question then is: can there be a good rate-based model of the brain, i.e., a model in which observables are rates, or is it necessary to include spikes in the set of observables? The question has little to do with the question of coding (how much information there is in either spike timing or rates about some other observable). It has to do with whether rates, as observables, sufficiently characterize the natural system so that the evolution of a formal system based on them can be mapped to the evolution of the natural system. In other words: do rates have a causal value in the dynamics of neural networks? It is easy to imagine how spikes might, because neurons (mainly) communicate with spikes and there are some biophysical descriptions of the effect of a single spike on various biophysical quantities. It is not so easy for rates. The problem is that in our current biophysical understanding of neurons, spikes are observables that have a causal role (e.g. the notion of a postsynaptic potential), but rates are primarily described as observables (averages of some sort) with no causal nature. To support rate-based theories is to demonstrate the causal nature of rates. As far as I know, it has not been done, and I have heard no convincing reason why rates might have a causal nature.

In fact, given that a rate is an observable that is defined on top of another observable, spikes, the question reduces to a more formal question, about relations between two formal systems: can a spike-based model of the brain be approximated by a rate-model? (in the same sense as depicted on the figure above) This is an interesting remark, because now the question is not primarily empirical but formal, and therefore it can be addressed theoretically. In fact, this question has already been addressed. This is precisely the goal of all studies trying to derive mean-field descriptions of spiking neural networks. So far, the results of those studies are that 1) it is not possible in the general case; 2) it is possible under some specific assumptions about the structure of the spiking model, which are known not to be empirically valid (typically: random sparse connectivity, independent external noise to all neurons).