In cortical neurons, and probably in most vertebrate neurons, spikes recorded at the soma look “sharp”, ie, the voltage suddenly rises, unlike the more gradual increase seen in standard biophysical models (eg the Hodgkin-Huxley model of the squid giant axon). Recently I reviewed that phenomenon and current explanations. My own explanation, which I called the “compartmentalization of spike initiation”, is related to the fact that the main outward current at spike initiation (where “outward” is relative to the initiation site) is not the transmembrane K+ current but the axial current flowing between the axonal initiation site and the soma (see the original paper where I explain it). An important consequence is that the proportion of open Na+ channels is a discontinuous function of somatic voltage. In other words, spikes are initiated as in an integrate-and-fire model.

I came up with a few simple illustrations to explain what “sharp” initiation means. Imagine that the somatic membrane potential is represented by a ball moving on a landscape:

Synaptic inputs can make the ball move to right (red, excitation) or to the left (blue, inhibition). If the input moves the ball past the top of the hill, then the ball will continue going down the hill without any additional excitation: it's a spike.

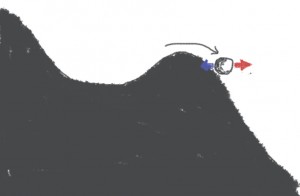
This is more or less the standard account of spike initiation. Note that if the ball is just past the hill, then it is possible to make it move back with an appropriate amount of inhibition. Sharpness here is represented by the steepness of the slope: a steeper slope will give faster spikes, and will also make it more difficult to go back once the hill has been passed.

What I proposed is that the correct drawing is rather this:

When the ball goes past the hill, the ball falls:

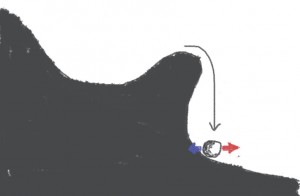
This occurs quickly, and importantly, there is a point after which there is no possible coming back. So the situation is qualitatively different from the standard account of spike initiation: it's not just that the slope is more or less steep, but rather there is a ravine.

You will note that there is a short distance between the top of the hill and the ravine, where the ball is pushed towards the ravine but not irreversibly. This corresponds to the persistent sodium current near spike initiation, which comes from the axon.

A couple of years ago, I proposed a new view on the initiation of spikes, which explains why spike initiation is “sharp” - i.e., spikes seem to rise suddenly rather than gradually. I reviewed that hypothesis recently along with two other hypotheses. I have found it quite difficult to explain it in a simple way, without relying on the equations. After reading the description of spike initiation in a textbook (Purves), I came up with a possibly simpler explanation.

In Purves et al. “Neuroscience”, you find the following description, which is based mostly on the work of Hodgkin and Huxley on squid giant axons:

The threshold is that value of membrane potential, in depolarizing from the resting potential, at which the current carried by Na+ entering the neuron is exactly equal to the K+ current that is flowing out. Once the triggering event depolarizes the membrane beyond this point, the positive feedback loop of Na+ entry on membrane potential closes and the action potential “fires”.

This description corresponds to an isopotential model of neuron. There is an ambiguity in it, which is that initiation actually occurs when the sum of Na+ current and stimulation current (electrode or synaptic) equals the K+ current, so the description is correct only if the current is a short pulse (otherwise for a current step the threshold would be lower).

The active backpropagation hypothesis, put forward by David McCormick to explain the sharpness of spike initiation is as follows: a spike is initiated as described above in the axon, and then it actively backpropagated (that is, with Na channels) to the soma. On its way to the soma, its shape becomes sharper. I discussed in my review why I think this explanation is implausible, but it is not the point of this post.

The compartmentalization hypothesis that I proposed differs in an important way from the textbook explanation above. The site of initiation is very close to the soma, which is big, and the axonal initial segment is very small. This implies that the soma is a “current sink” for the initiation site: this means that when the axon is depolarized at the initiation site, the main outgoing current is not the K+ current (through the axonal membrane) but the resistive current to the soma. So the textbook description is amended as follows:

The threshold is that value of membrane potential, in depolarizing the soma from the resting potential, at which the current carried by Na+ entering the axonal initial segment is exactly equal to the resistive current that is flowing out to the soma. Once the triggering event depolarizes the membrane beyond this point, the positive feedback loop of Na+ entry on membrane potential closes and the action potential “fires”.

The difference is subtle but has at least two important consequences. The first one is that the voltage threshold does not depend on the stimulation current, and so the concept of voltage threshold really does make sense. The second one is that the positive feedback is much faster with compartmentalized initiation. The reason is that in the isopotential case (explanation 1), charging time is the product of membrane resistance and membrane capacitance, which is a few tens of milliseconds, while in the compartmentalized case, it is the product of axial resistance and membrane capacitance. The membrane capacitance of the axon initial segment is small because its surface is small (and the axial resistance is not proportionally larger). This makes the charging time several orders of magnitude smaller in the compartmentalized case.