Neurons communicate primarily with spikes, which are discrete events, but most computational neuroscience deals with spike rates, which are continuous variables (see my blog posts on this debate). I am interested in understanding neural computation at the spike level. Some of this is described in my Habilitation thesis, written in 2009: "Spike-based models of neural computation". See also my presentation (in French) at the Collège de France on time in neural computation.
Properties of spiking neuron models
I have developed a mathematical theory of one-dimensional integrate-and-fire models driven by time-varying inputs (3,5), including periodic inputs (1,3), which can explain how these models can produce reproducible spike trains (2). This work shows how these models encode inputs into trains of precisely timed spikes. Recently, using simple models and slice recordings, we showed that neurons also have the complementary property, that is, they are extremely sensitive to coincidences in even a very small proportion of their inputs (13). Together, these two properties suggest a simple neural circuit to detect the similarity between two signals, a mechanism that can be used to extract the structure of sensory signals (15):
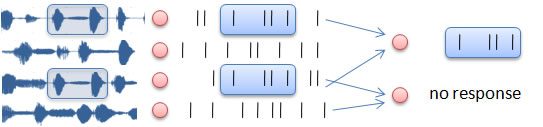
This operation is based on stimulus-specific synchrony, a notion that is not identical to correlation.
What spiking model to use?
With Wulfram Gerstner, I proposed a bidimensional integrate-and-fire model named the adaptive exponential integrate-and-fire model (4,7), which can exhibit a variety of electrophysiological signatures such as bursting, spike-frequency adaptation, rebound, etc. Jonathan Touboul and I analyzed the dynamics of this model (6,8), where we describe the electrophysiological classes defined by the parameters.
By fitting various spiking models to intracellular recordings (with somatic fluctuating current injection), we found that adaptive integrate-and-fire models could predict cortical spike trains very well, at a millisecond timescale (9,11). Interestingly, the optimization procedure predicts a very sharp threshold, much sharper than expected from single-compartment Hodgkin-Huxley models; Izhikevich model was also found less precise on this data. I showed that this is due to the fact that spikes are initiated in the axon initial segment, which effectively turns the neuron into an integrate-and-fire device (17,19).
Spike initiation and threshold dynamics
An often neglected aspect is that this spike threshold is not a fixed quantity, but depends on the stimulation. With Jonathan Platkiewicz, we found that only two mechanisms could explain its observed properties: sodium channel inactivation and strong adaptive voltage-gated conductances (e.g. K+) and we proposed a threshold equation which quantifies the contribution of all these mechanisms (10), which was later shown to predict spike threshold dynamics in vivo (18). We introduced the concept of the "effective postsynaptic potential" (difference between PSP and threshold) to understand the integrative properties with an adaptive threshold, such as enhanced coincidence detection (12). I also showed how a model with adaptive threshold can produce responses that do not depend on input amplitude (14). We used this model to predict the responses of auditory neurons to sounds with various levels (16).
Relevant publications (chronological order):
- Brette, R. (2003). Rotation numbers of discontinuous orientation-preserving circle maps. Set-Valued Analysis 11(4): 359-371.
- Brette, R. and E. Guigon (2003). Reliability of spike timing is a general property of spiking model neurons. Neural Comput 15(2): 279-308.
- Brette, R. (2004). Dynamics of one-dimensional spiking neuron models. J Math Biol 48(1): 38-56.
- Brette, R. and W. Gerstner (2005). Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J Neurophysiol 94: 3637-3642.
- Brette, R. (2008). The Cauchy problem for one-dimensional spiking neuron models. Cognitive Neurodynamics 2(1) 21-27.
- Touboul, J. and R. Brette (2008). Dynamics and bifurcations of the adaptive exponential integrate-and-fire model. Biological Cybernetics 99(4-5):319-34. (code)
- Gerstner, W. and R. Brette (2009) Adaptive exponential integrate-and-fire model. Scholarpedia, 4(6):8427.
- Touboul, J. and R. Brette (2009). Spiking dynamics of bidimensional integrate-and-fire neurons. SIAM J. Appl. Dyn. Syst. 8(4): 1462-1506.
- Rossant C, Goodman DF, Platkiewicz J and Brette R (2010).Automatic fitting of spiking neuron models to electrophysiological recordings. Front. Neuroinform. doi:10.3389/neuro.11.002.2010
- Platkiewicz J, Brette R (2010) A Threshold Equation for Action Potential Initiation. PLoS Comput Biol 6(7): e1000850. doi:10.1371/journal.pcbi.1000850.
- Rossant C, Goodman DF, Fontaine B, Platkiewicz J, Magnusson AK and Brette R (2011). Fitting neuron models to spike trains.Front Neurosci. 5:9. doi: 10.3389/fnins.2011.00009.
- Platkiewicz J, Brette R (2011). Impact of Fast Sodium Channel Inactivation on Spike Threshold Dynamics and Synaptic Integration. PLoS Comp Biol 7(5): e1001129. doi:10.1371/journal.pcbi.1001129.
- Rossant C, Leijon S, Magnusson AK, Brette R (2011). Sensitivity of noisy neurons to coincident inputs. J Neurosci 31(47):17193-17206.
- Brette R (2012). Spiking models for level-invariant encoding. Front Comput Neurosci. 5:63. doi: 10.3389/fncom.2011.00063.
- Brette R (2012). Computing with neural synchrony. PLoS Comp Biol. 8(6): e1002561. doi:10.1371/journal.pcbi.1002561. (code)
- Fontaine B, Benichoux V, Joris PX and Brette R (2013). Predicting spike timing in highly synchronous auditory neurons at different sound levels. J Neurophysiol 110(7):1672-88.
- Brette R (2013). Sharpness of spike initiation in neurons explained by compartmentalization. PLoS Comp Biol, doi: 10.1371/journal.pcbi.1003338.
- Fontaine B, Peña JL, Brette R (2014). Spike-threshold adaptation predicted by membrane potential dynamics in vivo. PLoS Comp Biol, 10(4): e1003560.
- Brette R (2015). What Is the Most Realistic Single-Compartment Model of Spike Initiation? PLoS Comput Biol. 2015 Apr 9;11(4):e1004114.
